

Epic pics







 |
My Sites | Song Of The Month |
|
My Sites | Song Of The Month |

Welcome to my hub, dear internet wanderer!
I'm Lepersonaf, and here you can view some fast-travels to my other sites.
I've got interested in making sites some time ago, so here I am,
making something again.
I have lot of plan for future, but I don't think i can make them all real.
This site is the main "hub" of my Neocities profile, from here you can get to every site I have ever made, including some unfisnihed works and in general abandoned stuff.
Anyway, lettuce... p r o c e e d.

My first site! (looks horrible af lmao)
My first attempt, or rather passion to create something. Just decided to put some of my favorite music here, but at one moment lost motivation :(.
It barely loads in everything i put in, hah.
--> The link to it
Da "Target" function
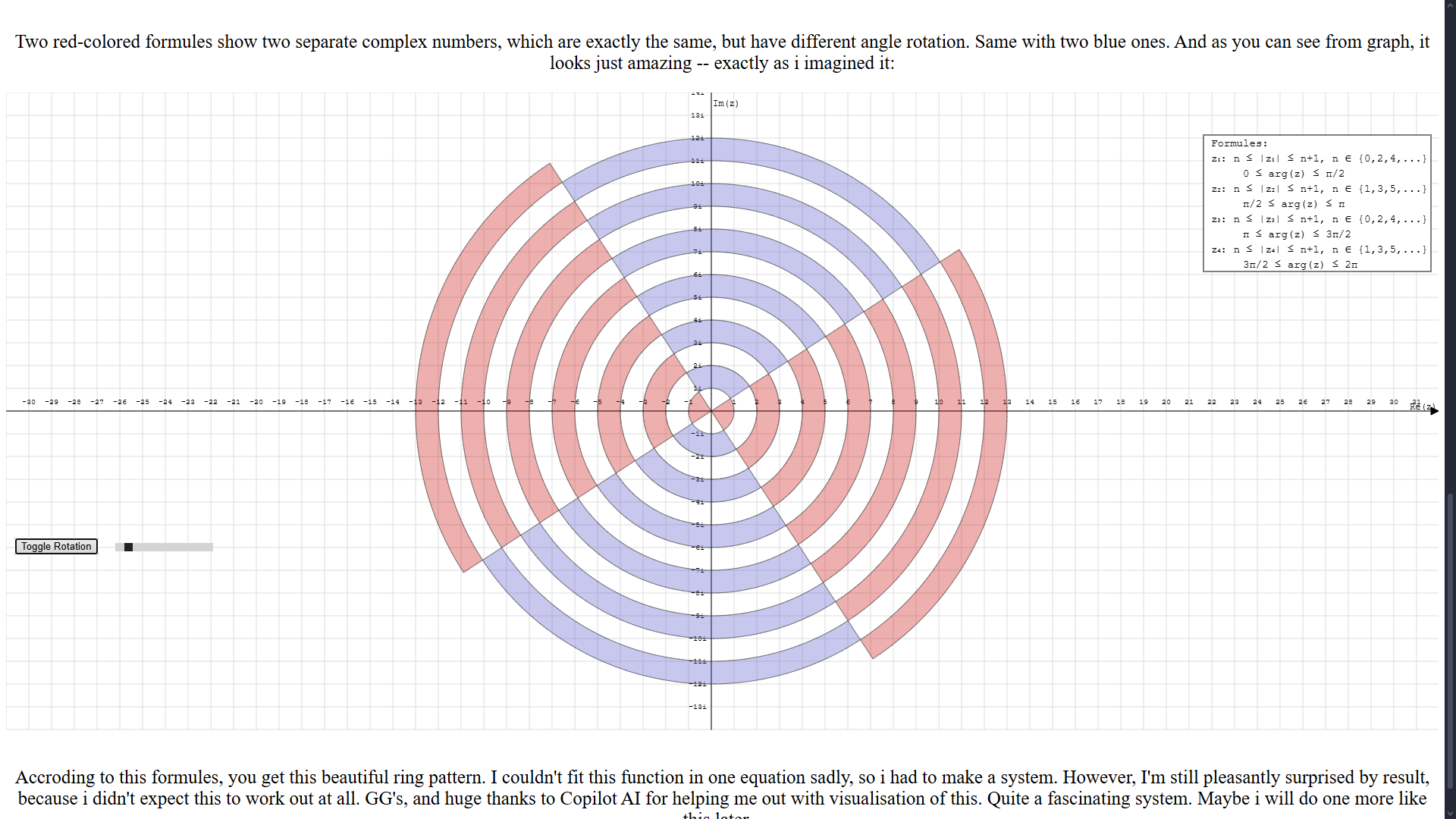
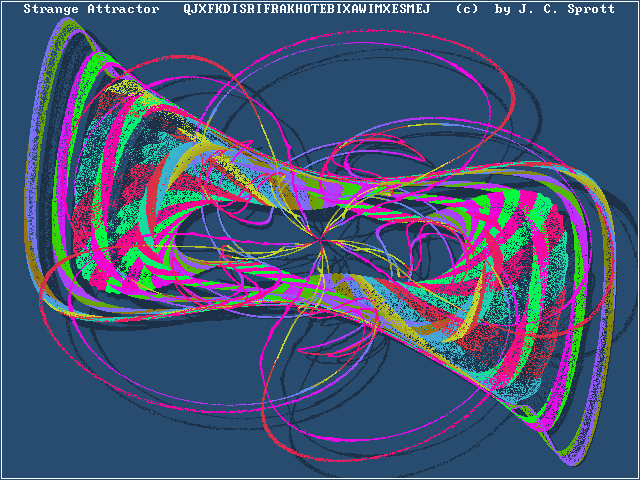
One day i was lying in my bed, thinking about graphs of imaginary numbers.
I was really fascinated by sector graph, like,
the way it was so obvious and yet beautiful.
And i began thinking about possibilites... And came up with that!
I didn't believe my idea will work, but with help of Copilot i have done it!
I really like this graph, even thought i couldn't fix site properly :p.
--> The link to it
Even more functions :0
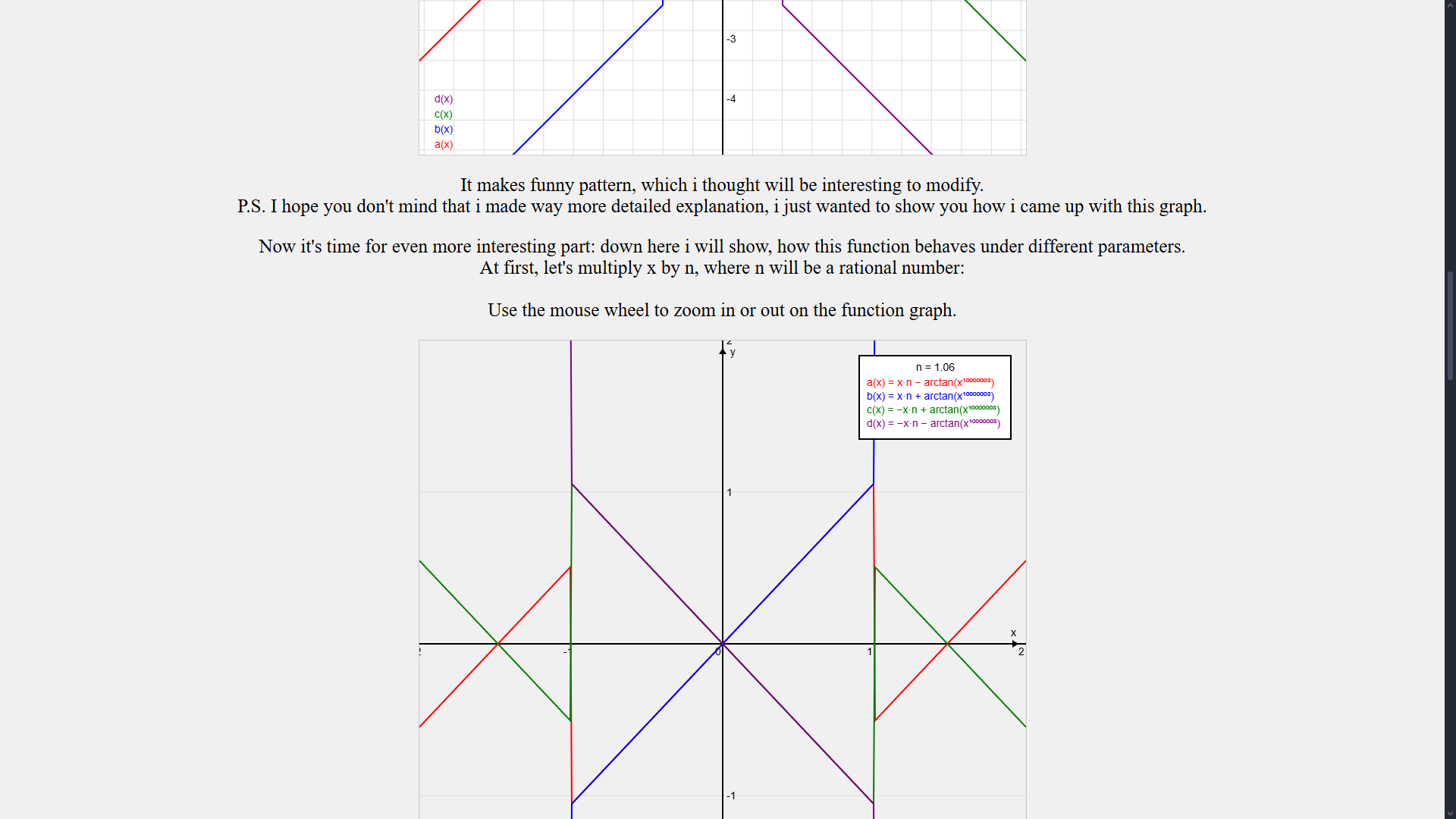
I was just sitting and solving some integrals when i got an interesting answer. After plotting it as function and messing around for some time,
I got an interesting graph, and was suprised by cool transoformations
with parameters. And with help of Copilot i made this site.
Took me some since i had to tackle with canvases and etc,
but I'm satisfied with the result. I didn't fix it properly, so it won't load as intended on mobile sadly. Yeah, I'm a lazy creature, how did you guess?
--> The link to it
This is the introduction to what i usually post here.
Not high-quality content, just what I feel like doing you know.
Sites List
There's a list of every site I made on this platform, so you can
(if you will even care) visit them.
It includes some 2 line sites which were made by mistake, so yeah.

Here I'm going to post my favorite song of this month, as simple as it is.
The song of this month is...
I've made my own button, feel free to use it!
That's it for now.
Epic sites